In diesem Blog Post möchte ich euch Bubble Sort vorstellen. Einer mit der einfachsten Sortieralgorithmen die es so gibt.
Bubble what?
Am besten stellt man sich den Sortieralgorithmus so vor: Blasen steigen in einem Medium nach oben und ordnen sich so in in richtiger Reihenfolge an. Die Blase kann man sich als konkretes Datum vorstellen welche vergleichbar mit anderen Daten sein muss.
In meinem Beispiel benutze ich Zahlen, da diese schon eine Ordnung besitzen. Im Prinzip kann man aber eigentlich fast alles benutzen was man ordnen kann.
int[] unsorted = {4, 13, 1, 9, 9, 2, 7, 3};
Oben: meine (noch) unsortierte Liste - welche mit BubbleSort sortiert werden soll.
Falls man sich jetzt vorstellt, man müsste obiges Array manuell mit BubbleSort sortieren, fängt man einfach vorne an. Jetzt vergleicht man 4 mit 13. Die 13 ist größer als die 4 also ist alles in Ordnung. Dann geht man eins weiter, und vergleicht die 13 mit der 1. Hier stellt man fest, dass die 13 größer ist wie die 1. Also lässt man die 13 aufsteigen indem man die 13 und die 1 vertauscht.
Angenommen wir hätten folgendes Array:
int[] unsorted = {13, 11, 7, 5, 3, 2};
Hier sehen wir sofort, die Reihe ist absteigend sortiert. Für eine aufsteigende Sortierung musss man jetzt jedes Element hochsteigen lassen.

Oben das noch unsortierte Array im schlechtesten Fall
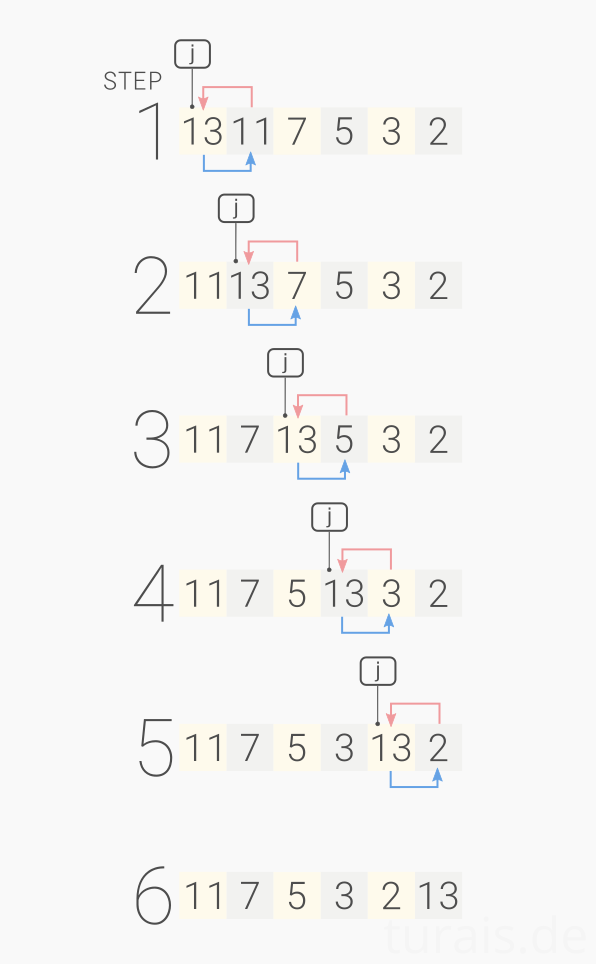
Wie man sieht, braucht man um einen Wert zu sortieren einen n-Durchlauf. In unserem Fall 6. Dies muss man jetzt für alle (n) Werte wiederholen. So kommen wir auf unsere Worst-Case Laufzeit von:
$$\mathcal{O}(n^{2})$$
Pseudocode
BUBBLESORT(B)
for i to B.length -1
for j:= 1 to B.length-1 do
if(A[j] > A[j+1])
swap(A[j], A[j+1])
Pseudocode von Bubblesort[1]
Natürlich kann man hier noch ein paar Verbeserungen vornehmen. Aber im groben ist das schon der BubbleSort.
Die äußere Schleife geht jedes Element durch, lässt dieses dann mit der inneren Schleife aufsteigen.
Java
In Java habe ich für die äußere Schleife eine while-Schleife gewählt, um sie abzubrechen falls in einem Durchlauf keine Vertauschungen mehr stattfinden.
private static void bubbleSort(int[] toSort) {
boolean done = false;
while (!done) {
done = true;
for (int i = 0; i < toSort.length-1; i++) {
int valA = toSort[i];
int valB = toSort[i+1];
if(valA > valB) {
done = false;
swap(i, i+1, toSort);
}
}
}
}
Meine Swap-Funktion schaut so aus:
private static void swap(int indx_a, int indx_b, int[]array) {
int value_a = array[indx_a];
array[indx_a] = array[indx_b];
array[indx_b] = value_a;
}
Und das ganze als komplette Klasse zum schnellen Copy-Pasten:
public class BubbleSort {
private static void bubbleSort(int[] toSort) {
boolean done = false;
while (!done) {
done = true;
for (int i = 0; i < toSort.length-1; i++) {
int valA = toSort[i];
int valB = toSort[i+1];
if(valA > valB) {
done = false;
swap(i, i+1, toSort);
}
}
}
}
private static void swap(int indx_a, int indx_b, int[]array) {
int value_a = array[indx_a];
array[indx_a] = array[indx_b];
array[indx_b] = value_a;
}
public static void main(String[] args) {
int[] unsorted = {4, 13, 1, 9, 9, 2, 7, 3};
System.out.println(Arrays.toString(unsorted));
bubbleSort(unsorted);
System.out.println(Arrays.toString(unsorted));
}
}
Introduction to Algorithms, 3rd ed., Cambridge, MA: MIT Press, 2009 ↩︎

If you press this Button it will Load Disqus-Comments. More on Disqus Privacy: Link