Dieser Beitrag gehört zu meiner Algorithmen-Serie, speziell zu den Sortieralgorithmen. Ich werde im folgenden den Insertion-Sort Algorithmus vorstellen und erklären. Dieser wird auch oft in der deutschen Literatur "Sortieren durch einfügen" genannt.
Prinzip
Stellt euch vor Ihr spielt Karten. Wie würdet Ihr eure Karten auf der Hand einsortieren?
Viele von euch, werden die Karten wahrscheinlich nach folgendem Prinzip sortieren. Nochmal die Annahme: Ihr habt Karten auf der Hand und sie sind unsortiert. Die Karten könnten ungefähr so aussehen:

Intuitiv Karten auf der Hand sortieren
Man wählt eine Karte aus, zum Beispiel Karte mit dem Wert 7. Die 7 würde man vor der 9 einsortieren. Eure Hand verhält sich eher wie eine verkettete Liste. In welche Ihr die 7 nun einfach zwischen die 1 und die 9 einhängen könnt. So würdet Ihr wahrscheinlich für alle anderen Karten fortfahren und dementsprechend einsortieren.
Array
Da der Speicher im Computer aber eine Array Struktur besitzt, könnte man sich auch vorstellen, man hätte Fächer vor sich. In diesen liegen nun die Karten. Jede Karte passt immer nur in ein Fach und man kann nur die Fächer links und rechts von dem betrachteten Fach sehen.

Oben: Array noch unsortiert
Wir gehen jetzt vom obigen Array aus. Hier würdet Ihr wahrscheinlich wieder irgendwo anfangen, diesmal z.B. bei der 1.
Beispiel anhand eines Durchlaufs
Im folgenden sortieren wir genau eine Karte an die richtige Position ein. Wir starten an beliebiger Stelle. Dies macht man später für den systematischen Durchlauf nicht.
Jetzt müsstet Ihr die 1 mit einem benachbarten Element vergleichen. Weiterhin nehmen wir nun an, dass wir immer mit dem linken Element vergleichen. Die 1 steht an Position i, dann wäre unser linkes Element an der Position i-1.
Wir nehmen unser Element i heraus und speichern uns den Wert zuerst in einer Variablen. val = A[i]. Man kann also annehmen, die Karte ist aus dem Array herausgenommen. An der Position i kann also etwas beliebiges stehen und ist beschreibbar ohne Informationsverlust.

Bild oben: Wir haben die 1 herausgenommen und vergleichen die 1 mit der 13.
Jetzt überprüft man, ob die 13 größer ist wie die 1.
Wenn der Wert kleiner wäre, dann wäre die 1 schon an der richtigen Position (für den Durchlauf).
In unserem Fall ist die 13 größer wie die 1, also kommt die 13 eins nach rechts.

Bild oben: Die 13 ist auf den freien Platz gewandert - unsere 1 wird mit der 4 verglichen.
Die 1 bleibt noch gemerkt, und wird nun mit der 4 verglichen. Da die 4 größer ist wie die 1, wird jetzt die 4 nach rechts verschoben.
Jetzt sind wir am Anfang des Arrays, deshalb können wir unseren Wert nur noch auf dem letzten Feld platzieren.

Bild oben: Die 4 ist nach rechts gewandert.
Die 4 ist jetzt eine Stelle nach rechts verschoben worden. Die 1 wird auf dem ersten Feld platziert.

Bild oben: Die 1 ist an den richtigen Platz "gewandert".
Insertion Sort Pseudocode
1.INSERTION_SORT(A):
2. FOR i = 1 to A.length -1 DO
3. val = A[i]
4. j = i - 1
5. WHILE j >= 0 AND A[j] > val DO
6. A[j+1] = A[j]
7. j = j - 1
8. OD
9. A[j+1] = val
10. OD
Schritt für Schritt
Zeile 2
FOR i = 1 to A.length -1 DO
Wir starten bei dem zweiten Element, damit es noch ein linkes Element gibt, welches wir vergleichen können.
Ich gehe immer davon aus, dass unser Array wie ein Array in den meisten Programmiersprachen angesprochen wird. Dies bedeutet, der erste Index ist die 0.
Zeile 3
val = A[i]
Hier speichern wir uns den aktuellen Wert in eine zusätzliche Variable, da wir in den folgenden Schritten die Elemente nach rechts rucken.
Zeile 4

Unsere zweite Schleifenvariable wird das j.
Zeile 5
Wir gehen jetzt von rechts nach links das Arraz durch. Da wir noch am Anfang des Arrays sind, läuft die Schleife genau einmal durch. Die Variable j ist 0.
Zeile 6
Das rechte Element A[j+1] auf das aktuelle Element gesetzt.
Zeile 7
Hier ziehen wir die 1 von j ab.
Zeile 9
Diese Zeile wird erst betrachtet, wenn das linke Element nicht mehr größer ist wie unseres Element val, deswegen haben wir den richtigen Platz gefunden. Dieser ist auch frei und beschreibbar, denn in der obigen Schleife wurden alle anderen Werte schon nach rechts verschoben.
Man muss nur wieder den Index inkrementieren, damit man die richtige Stelle beschreibt. Wir würden also nun, das Array an Stelle 0 beschreiben.
Konkretes Beispiel

Wenn wir obige Konstellation im ersten äußeren Schleifendurchlauf durchgehen, merkt man dass die innere Schleife nicht betreten wird. Denn die 13 ist größer wie die 4.
Dies ist der erste Step wie im unteren Bild zu erkennen.
Blaue Pfeile kennzeichnen den Wert, welcher einsortiert wird. Rote Pfeile kennzeichnen den Swap - also das verschieben nach rechts. Im jeweiligen Schritt wurden die Swaps nur gekennzeichnet, aber noch nicht durchgeführt.
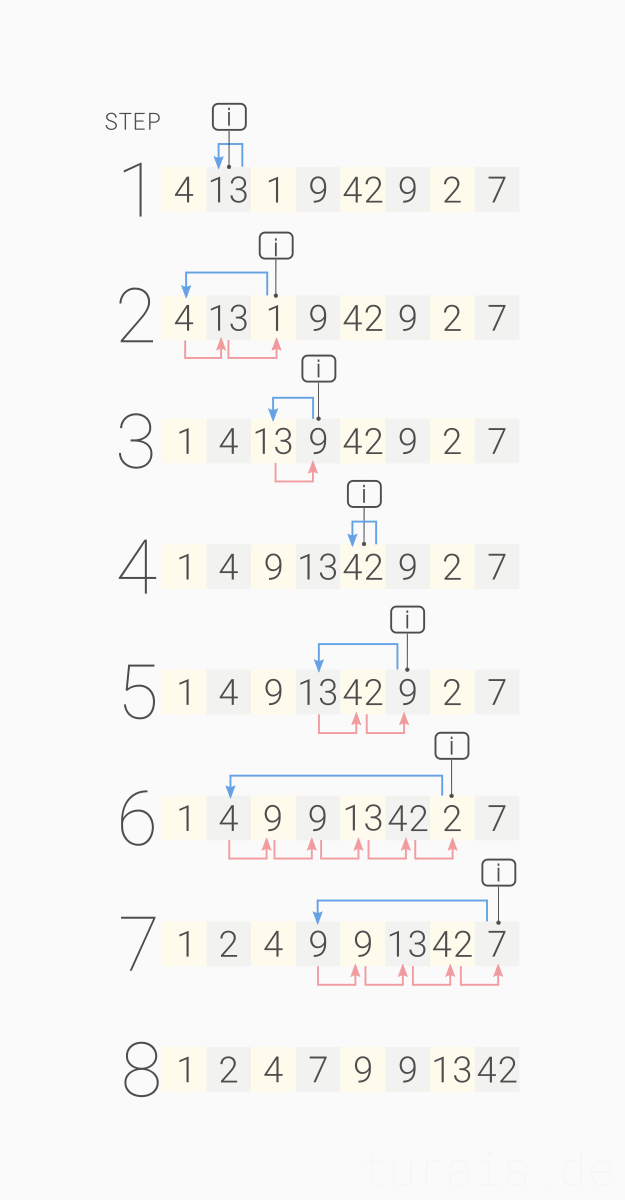
Bild oben: Alle äußeren Schleifendurchläufe in einem Bild.
Big-O - Laufzeitkomplexität
Ich möchte hier einfach auf folgende Seite verweisen. Sie bietet eine super Übersicht über alle Laufzeitkomplexitäten.
Big-O Cheat Sheet
Schlechtester Fall Laufzeitkomplexität:
$$\mathcal{O}(n^{2})$$
Insertion Sort Java Beispiel
private final static void insertionSort(int[] toSort) {
for (int i = 1; i < toSort.length; i++) {
int el = toSort[i];
int j = i-1;
while (j >= 0 && toSort[j] > el) {
toSort[j+1] = toSort[j];
j--;
}
toSort[j+1] = el;
}
}
Komplette Klasse zum Copy-Pasen und ausprobieren
import java.util.Arrays;
public class InsertionSort {
private static void insertionSort(int[] toSort) {
for (int i = 1; i < toSort.length; i++) {
int el = toSort[i];
int j = i-1;
System.out.println(i + ":" +Arrays.toString(toSort));
while (j >= 0 && toSort[j] > el) {
toSort[j+1] = toSort[j];
j--;
System.out.println("\t" + j + ": "+Arrays.toString(toSort));
}
toSort[j+1] = el;
}
}
public static void main(String[] args) {
int[] unsorted = {4, 13, 1, 9, 42, 9, 2, 7};
System.out.println(Arrays.toString(unsorted));
System.out.println("####################################");
insertionSort(unsorted);
System.out.println("####################################");
System.out.println(Arrays.toString(unsorted));
}
}


If you press this Button it will Load Disqus-Comments. More on Disqus Privacy: Link